Experiment #1 - Sphere Falling in Water
The situation of a sphere falling in water is a classic fluid dynamics problem. If the diameter and density of the sphere are known along with the fluid properties of water, then the terminal velocity of the sphere can be estimated.

Figure 1 - Sphere falling in water
Figure 1 shows the sphere at the water surface. The acceleration direction is shown in red.Analytical Solution
If a creeping flow is assumed (Reynold's number < 1) then the terminal velocity is
U = (sphere_density - water_density)*sphere_diameter^2*g / (18*water_viscosity)
For an example let
- sphere_density = 2,030 kg/m^3
- sphere_diameter = 0.0001 m
- water_density = 1,030 kg/m^3
- water_viscosity = 0.0020 N-s/m^2
- g = 9.81 m/s^2
Using the above values, the terminal velocity, assuming a creeping flow, is calculated as
U = (2,030 - 1,030)*(0.0001)^2*9.81 / (18*0.0020) = 0.002725 m/s
The calculated velocity must be checked with the Reynold's equation
Re = water_density*sphere_diameter*U / water_viscosity
Re = 1,030*0.0001*0.002725 / 0.002 = 0.140
Since Re < 1, the flow assumption is valid.
If the sphere diameter is larger, for example 0.1 m, then the velocity is calculated to be
U = (2,030 - 1,030)*(0.1)^2*9.81 / (18*0.0020) = 0.002725 m/s
Simulation
To set up the simulation, first define the simulation XML file.
single_sphere.xml
<?xml version="1.0"?> <World> <Environment> <Physics> <Engine engine="Newton" /> <Gravity x="0" y="-9.81" z="0" /> </Physics> <Water> <Dimensions width="25" length="50" /> <Texture file="../resources/bitmaps/water.bmp" /> </Water> <Visibility> <Fog density="0.0" depth="100" /> </Visibility> </Environment> <WorldObjects> <WorldObject file="sphere.xml" /> </WorldObjects> </World>
sphere.xml
<?xml version = "1.0"?> <WorldObject name = "sphere"> <Origin x="0" y="0" z="0"/> <Graphics> <Model file="sphere.ms3d" /> <Origin x="0" y="0" z="0" /> <Scale x= "0.05" y= "0.05" z="0.05" /> </Graphics> <Physics> <Watch type="position" file="sphere_position.csv" interval="0.01" /> <Primitives> <Sphere name="sphere"> <Position x="0" y="0" z="0" /> <Dimensions radius="0.0001" /> <Mass mass= "0.0099999998" /> </Sphere> </Primitives> </Physics> </WorldObject>
Results
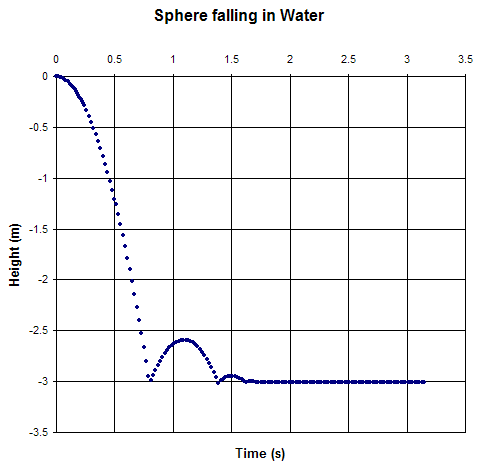
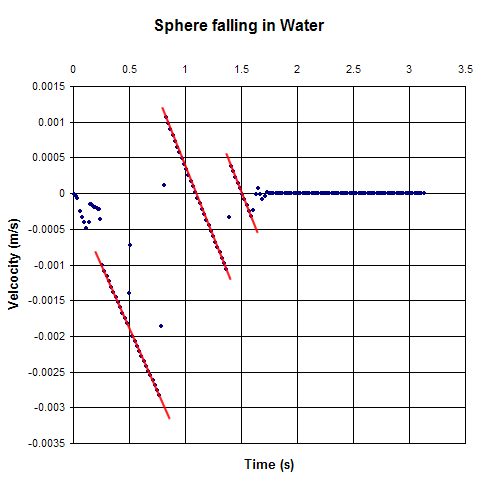
Figure One shows the position of the sphere plotting with respect to time.